Data Challenge Lab Home
Model evaluation [model]
(Builds on: Models with multiple variables)
library(tidyverse)
library(modelr)
A crucial part of the modeling process is determining the quality of your model. In this reading, we’ll explore how to compare different models to each other and pick the one that best approximates your data.
The problem
In order to illustrate the process of model evaluation, we’re going to use simulated data. To simulate data, you pick a function and use that function to generate a series of data points. We can then compare any models we make to the true function used to generate the data.
Note that you almost always won’t actually know the functional representation underlying your data. If you did, you probably wouldn’t need a model in the first place.
For our simulated data, let’s assume there’s some phenomenon that has a functional representation of the form
y = f(x)
In other words, the phenomenon is purely a function of the variable x,
and so, if you know x, you can figure out the behavior of the
phenomenon. Here’s the function f() that we’ll use.
# True function
f <- function(x) x + 50 * sin((pi / 50) * x)
f() is the true function, but let’s also assume that any measurements
of y will have errors. To simulate errors, we need a function that
adds random noise to f(). We’ll call this function g().
# Function with measurement error
g <- function(x) f(x) + rnorm(n = length(x), mean = 0, sd = 20)
We can use g() to generate a random sample of data.
# Function that generates a random sample of data points, using g()
sim_data <- function(from, to, by) {
tibble(
x = seq(from = from, to = to, by = by),
y = g(x)
)
}
# Generate random sample of points to approximate
set.seed(439)
data_1 <- sim_data(0, 100, 0.5)
Here’s a plot of both the simulated data (data_1), and the true
function. Our job is now to use the simulated data to create a function
that closely approximates the true function.
tibble(x = seq(0, 100, 0.5), y = f(x)) %>%
ggplot(aes(x, y)) +
geom_line() +
geom_point(data = data_1) +
labs(title = "True function and simulated data")

The loess() model
Given the shape of our data, the stats::loess() function is a good
place to start. loess() works by creating a local model at each data
point. Each of these local models only uses data within a given distance
from that point. The span parameter controls how many points are
included in each of these local models. The smaller the span, the fewer
the number of points included in each local model.
To better understand the effect of the span parameter, let’s plot
loess() models with different values of span.
The function plot_loess() fits a model using loess(), then plots the
model predictions and the underlying data.
# Plot loess model for given span
plot_loess <- function(span) {
data_1 %>%
mutate(f = f(x)) %>%
add_predictions(loess(y ~ x, data = data_1, span = span)) %>%
ggplot(aes(x)) +
geom_line(aes(y = f)) +
geom_point(aes(y = y)) +
geom_line(aes(y = pred), color = "#3366FF", size = 1) +
labs(
title = str_glue("loess, span = {span}"),
y = "y"
)
}
Now, we can use purrr to apply plot_loess() to a vector of different
span values.
c(10, 1, 0.75, 0.1, 0.01) %>%
map(plot_loess) %>%
walk(print)

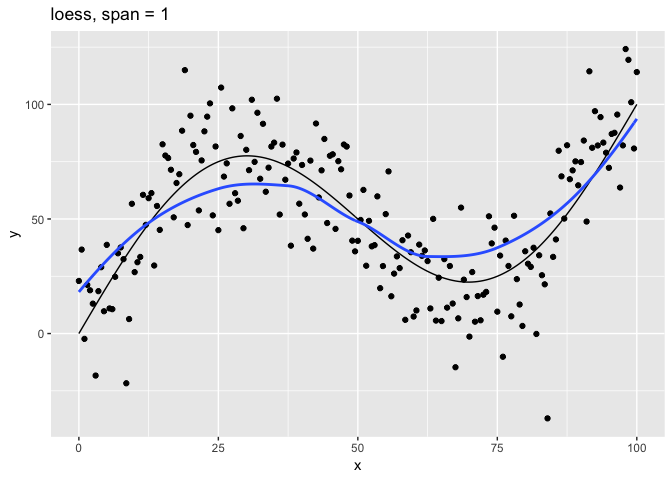



The span parameter clearly makes a big difference in the model:
span = 10smooths too much and washes out the variability in the model.span = 1is much better, but still has a bit too much smoothing.span = 0.75is the default and does a reasonably good job.span = 0.1has too little smoothing. The added complexity has started tracking the random variation in our data.span = 0.01went way too far and started to fit individual random points.
It’s clear that the model with span = 0.75 comes closest to following
the form of the true model. The models with span equal to 0.1 and
0.01 have overfit the data, and so won’t generalize well to new
data.
Test and training errors
Let’s return to the question of how to measure the quality of a model.
Above, we could easily visualize our different models because they each
had only one predictor variable, x. It will be much harder to
visualize models with many predictor variables, and so we need a more
general way of determining model quality and comparing models to each
other.
One way to measure model quality involves comparing the model’s predicted values to the actual values in data. Ideally, we want to know the difference between predicted and actual values on new data. This difference is called the test error.
Unfortunately, you usually won’t have new data. All you’ll have is the data used to create the model. The difference between the predicted and actual values on the data used to train the model is called the training error.
Since the expected value for the error term of g() is 0 for each
x, the best possible model for new data would be f() itself. The
error on f() itself is called the Bayes error.
Usually, you won’t know the true function f(), and you won’t have
access to new test data. In our case, we simulated data, so we know
f() and can generate new data. The following code creates 50 different
samples, each the same size. We’ll use these 50 different samples to get
an accurate estimate of our test error.
set.seed(886)
data_50 <-
1:50 %>%
map_dfr(~ sim_data(0, 100, 0.5))
Now, we need a way to measure the difference between a vector of predictions and vector of actual values. Two common metrics include:
- Root-mean-square error (RMSE):
sqrt(mean((y - pred)^2, na.rm = TRUE)) - Mean absolute error (MAE):
mean(abs(y - pred), na.rm = TRUE)
Both measures are supported by modelr. We’ll use RMSE below.
Now, we’ll train a series of models on our original dataset, data_1,
using a range of span’s. Then, for each model, we’ll calculate the
training error on data_1 and the test error on the new data in
data_50.
First, we need to create a vector of different span values.
spans <- 2^seq(1, -2, -0.2)
Next, we can use purrr to iterate over the span values, fit a model for each one, and calculate the RMSE.
errors <-
tibble(span = spans) %>%
mutate(
train_error =
map_dbl(span, ~ rmse(loess(y ~ x, data = data_1, span = .), data_1)),
test_error =
map_dbl(span, ~ rmse(loess(y ~ x, data = data_1, span = .), data_50))
)
The result is a tibble with a training error and test error for each
span.
errors
## # A tibble: 16 x 3
## span train_error test_error
## <dbl> <dbl> <dbl>
## 1 2 27.7 27.4
## 2 1.74 26.9 26.7
## 3 1.52 25.9 25.7
## 4 1.32 24.6 24.6
## 5 1.15 22.8 23.0
## 6 1 21.3 21.8
## 7 0.871 19.3 20.4
## 8 0.758 18.7 20.2
## 9 0.660 18.5 20.2
## 10 0.574 18.4 20.3
## 11 0.5 18.4 20.3
## 12 0.435 18.3 20.4
## 13 0.379 18.1 20.4
## 14 0.330 17.8 20.4
## 15 0.287 17.4 20.6
## 16 0.25 17.2 20.8
It would be useful to compare these errors to the Bayes error, the error
on the true function, which you can think of as the “best-case-scenario”
error. The RMSE Bayes error is 20, the standard deviation of the random
errors added by g(). We can check this with an approximation using
data_50.
bayes_error <- 20
data_50 %>%
summarize(bayes_error = sqrt(mean((y - f(x))^2, na.rm = TRUE))) %>%
pull(bayes_error)
## [1] 19.9741
Now, let’s plot the training, test, and Bayes errors by span.
bayes <- tibble(
span = range(errors$span),
type = "bayes_error",
error = bayes_error
)
errors %>%
gather(key = type, value = error, -span) %>%
ggplot(aes(1 / span, error, color = type)) +
geom_line(data = bayes) +
geom_line() +
geom_point() +
labs(
title = "Errors as a function of increasing model complexity",
color = NULL
)

Mapping 1 / span to the x-axis makes the plot easier to interpret
because smaller values of span create more complex models. The
leftmost points indicate the simplest models, and the rightmost indicate
the most complex.
The lowest test error is around 20.18, and came from the model with
span ≈ 0.758. Note that the default value of span in loess() is
0.75, so the default here would have done pretty well.
You can see that as the model increases in complexity, the training
error (blue line) continually declines, but the test error (green line)
actually starts to increase. The test error increases for values of
span that make the model too complex overfit the training data.
We used data_50, our new data, to calculate the actual test error. As
we’ve said, though, you usually won’t have access to new data and so
won’t be able to calculate the test error. You’ll need a way to
estimate the test error using the training data. As our plot indicates,
however, the training error is a poor estimate of the actual test error.
In the next section, we’ll discuss a better way, called
cross-validation, to estimate the test error from the training data.
Cross-validation
There are two key ideas of cross-validation. First, in the absence of new data, we can hold out of a random portion of our original data (the test set), train the model on the rest of the data (the training set), and then test the model on test set. Second, we can generate multiple train-test pairs to create a more robust estimate of the true test error.
modelr provides two functions for generating these train-test pairs:
crossv_mc() and crossv_kfold(). We’ll introduce these functions in
the next section.
Generating train-test pairs with crossv_mc() and crossv_kfold()
crossv_mc() and crossv_kfold() both take your original data as input
and produce a tibble that looks like this:
data_1 %>%
crossv_kfold()
## # A tibble: 5 x 3
## train test .id
## <list> <list> <chr>
## 1 <S3: resample> <S3: resample> 1
## 2 <S3: resample> <S3: resample> 2
## 3 <S3: resample> <S3: resample> 3
## 4 <S3: resample> <S3: resample> 4
## 5 <S3: resample> <S3: resample> 5
Each row represents one train-test pair. Eventually, we’re going to build a model on each train portion, and then test that model on each test portion.
crossv_mc() and crossv_kfold() differ in how they generate the
train-test pairs.
crossv_mc() takes two parameters: n and test. n specifies how
many train-test pairs to generate. test specifies the portion of the
data to hold out each time. Importantly, crossv_mc() pulls randomly
from the entire dataset to create each train-test split. This means that
the test sets are not mutually exclusive. A single point can be present
in multiple test sets.
crossv_kfold() takes one parameter: k, and splits the data into k
exclusive partitions, or folds. It then uses each of these k folds
as a test set, with the remaining k - 1 folds as the training set. The
main difference between crossv_mc() and crossv_kfold() is that the
crossv_kfold() test sets are mutually exclusive.
Now, let’s take a closer look at how these functions works. The
following code uses crossv_kfold() to create 10 train-test pairs.
set.seed(122)
df <-
data_1 %>%
crossv_kfold(k = 10)
df
## # A tibble: 10 x 3
## train test .id
## <list> <list> <chr>
## 1 <S3: resample> <S3: resample> 01
## 2 <S3: resample> <S3: resample> 02
## 3 <S3: resample> <S3: resample> 03
## 4 <S3: resample> <S3: resample> 04
## 5 <S3: resample> <S3: resample> 05
## 6 <S3: resample> <S3: resample> 06
## 7 <S3: resample> <S3: resample> 07
## 8 <S3: resample> <S3: resample> 08
## 9 <S3: resample> <S3: resample> 09
## 10 <S3: resample> <S3: resample> 10
The result is a tibble with two list-columns: train and test. Each
element of train and test is a resample object, which you might not
have seen before. Let’s look at the first row, the first train-test
pair.
train_01 <- df$train[[1]]
train_01
## <resample [180 x 2]> 1, 3, 4, 5, 6, 7, 9, 10, 11, 12, ...
test_01 <- df$test[[1]]
test_01
## <resample [21 x 2]> 2, 8, 21, 43, 53, 63, 78, 81, 85, 101, ...
Each resample object is actually a two-element list.
glimpse(train_01)
## List of 2
## $ data:Classes 'tbl_df', 'tbl' and 'data.frame': 201 obs. of 2 variables:
## ..$ x: num [1:201] 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 ...
## ..$ y: num [1:201] 22.95 36.64 -2.32 21.26 18.88 ...
## $ idx : int [1:180] 1 3 4 5 6 7 9 10 11 12 ...
## - attr(*, "class")= chr "resample"
The first element, data is the original dataset. The second element,
idx, is a set of indices that indicate the subset of the original data
to use.
We can use a set operation to verify that the train and test sets are mutually exclusive. In other words, there is no point in a given train set that is also in its corresponding test set, and vice versa.
is_empty(intersect(train_01$idx, test_01$idx))
## [1] TRUE
The union of each train and test set is just the complete original dataset. We can verify this by checking that the set of all train and test indices contains every possible index in the original dataset.
setequal(union(train_01$idx, test_01$idx), 1:201)
## [1] TRUE
resample objects are not tibbles. Some model functions, like lm(), can
take resample objects as input, but loess() cannot. In order to use
loess(), we’ll need to turn the resample objects into tibbles.
as_tibble(test_01)
## # A tibble: 21 x 2
## x y
## <dbl> <dbl>
## 1 0.5 36.6
## 2 3.5 18.5
## 3 10 26.8
## 4 21 79.3
## 5 26 68.5
## 6 31 102.
## 7 38.5 76.4
## 8 40 73.6
## 9 42 37.1
## 10 50 40.5
## # … with 11 more rows
Resample objects waste a lot of space, since each one contains the full dataset. A new package rsample is being developed to support tidy modeling in a more space-efficient way.
Process
crossv_kfold() and crossv_mc() just generate train-test pairs. In
order to carry out cross-validation, you still need to fit your model on
each train set and then evaluate it on each corresponding test set. In
this section, we’ll walk you through the process.
1 Create a function to calculate your test error
First, you’ll need a function that calculates the test error using some metric. We’ll use RMSE. The following function returns the RMSE for a given span, train set, and test set.
rmse_error <- function(span, train, test) {
rmse(loess(y ~ x, data = as_tibble(train), span = span), as_tibble(test))
}
2 Create a function to calculate CV error
Next, you need a function that iterates over all your train-test pairs, calculates the test error for each pair, and then calculates the mean of the errors and the standard error of the mean.
span_error <- function(span, data_cv) {
errors <-
data_cv %>%
select(-.id) %>%
add_column(span = span) %>%
pmap_dbl(rmse_error)
tibble(
span = span,
error_mean = mean(errors, na.rm = TRUE),
error_se = sd(errors, na.rm = TRUE) / sqrt(length(errors))
)
}
3 Create your train-test pairs
Use either crossv_mc() or crossv_kfold() to generate your train-test
pairs. We’ll use crossv_mc() to generate 10 train-test pairs with test
sets consisting of approximately 20% of the data.
set.seed(430)
data_mc <- crossv_mc(data_1, n = 10, test = 0.2)
4 Calculate the CV error for different values of your tuning parameter
We want to compare different values of span, so we also need to
iterate over a vector of different span values. We’ll calculate the CV
error for all spans using these train-test pairs.
errors_mc <-
spans %>%
map_dfr(span_error, data_cv = data_mc)
errors_mc %>%
knitr::kable()
| span | error_mean | error_se |
|---|---|---|
| 2.0000000 | 28.77162 | 0.4598847 |
| 1.7411011 | 27.90898 | 0.4590082 |
| 1.5157166 | 26.80809 | 0.4633976 |
| 1.3195079 | 25.42115 | 0.4763469 |
| 1.1486984 | 23.47827 | 0.5162414 |
| 1.0000000 | 21.89512 | 0.5574787 |
| 0.8705506 | 19.70633 | 0.6247474 |
| 0.7578583 | 19.00509 | 0.6083815 |
| 0.6597540 | 18.79978 | 0.5899732 |
| 0.5743492 | 18.80655 | 0.5736369 |
| 0.5000000 | 18.82917 | 0.5663217 |
| 0.4352753 | 18.87305 | 0.5575942 |
| 0.3789291 | 18.85135 | 0.5313073 |
| 0.3298770 | 18.78642 | 0.4918808 |
| 0.2871746 | 18.72327 | 0.5003602 |
| 0.2500000 | 18.70617 | 0.5152749 |
5 Choose the best model
Now, we need to compare the different models and choose the best value
of span.
Because we simulated our data, we can compare the CV estimates of the test error with the actual test error.
errors_mc %>%
left_join(errors, by = "span") %>%
ggplot(aes(1 / span)) +
geom_line(aes(y = test_error, color = "test_error")) +
geom_point(aes(y = test_error, color = "test_error")) +
geom_line(aes(y = error_mean, color = "mc_error")) +
geom_pointrange(
aes(
y = error_mean,
ymin = error_mean - error_se,
ymax = error_mean + error_se,
color = "mc_error"
)
) +
labs(
title = "Cross-validation and test errors",
y = "error",
color = NULL
)

From this plot, we can see that CV error estimates from crossv_mc()
underestimate the true test error in the range with 1/span > 1. The
line ranges reflect one standard error on either side of the mean error.
Usually, you won’t have access to the true test error, so we need a way
to choose the best value of span using just the CV errors. Here’s the
rule-of-thumb for choosing a tuning parameter when you only know the CV
errors.
- Start with the parameter that has the lowest mean CV error. In this
case, that would be
span= 0.25 (on the plot,1/span= 4) with an mean CV error of approximately 18.7. - Then choose the simplest model whose mean CV error is within one
standard error of the lowest value. The standard error for
span= 0.25 is approximately 0.5, so we are seeking the simplest model with a mean CV error less than 19.2. This occurs forspan≈ 0.758 (on the plot,1/span≈ 1.32).
We saw above that if we knew the test error, we would choose span ≈
0.758 as the optimal parameter. The one-standard-error rule of thumb
would lead us to choose the same optimal parameter without having to
know the test error. The test error for this span is very close to the
Bayes error of 20.
errors %>%
top_n(-1, test_error) %>%
select(span, test_error) %>%
knitr::kable()
| span | test_error |
|---|---|
| 0.7578583 | 20.1787 |